Методические элементы введения комбинаторики

Получили 27 чисел.

Ответ:

1) 6;

2) 27.

Упражнения:

1. Сколько подарочных наборов можно составить:

1) из одного предмета;

2) из двух предметов, если в наличии имеются одна ваза и одна ветка сирени?

2. Сколькими способами Петя и Вова могут занять 2 места за одной двухместной партой?

3. Сколько различных по комплекции парфюмерных наборов из 2 предметов можно составить, если в наличии имеются одинаковые флаконы одеколона и одинаковые куски мыла?

4. С помощью цифр 2 и 3 запишите всевозможные двузначные числа, в которых:

1) цифры должны быть разными;

2) цифры могут повторяться.

5. Имеются помидоры (П), огурцы (О) и лук (Л). Сколько различных салатов можно приготовить, если в каждый из них должны входить в равных долях два ингредиента? Запишите все сочетания овощей в составляемых салатах.

6. Имеются три предмета: карандаш, тетрадь и линейка. Сколькими способами из этих канцелярских принадлежностей можно выбрать:

1) один предмет;

2) три предмета;

3) два предмета?

7. Боря идет на день рождение к одноклассникам, близнецам Алеше и Яше. Он хочет подарить каждому из них по мячу. В магазине остались для продажи только 3 мяча: белый, черный и пятнистый. Сколькими способами, купив 2 мяча, Боря может сделать подарки братьям?

8. Ашот (А), Марат (М) и Сергей (С) могут занять 1-е, 2-е и 3-е призовые места в соревнованиях. Перечислите все возможные последовательности из имен мальчиков, где порядковый номер в последовательности соответствует занятому мальчиком месту в соревнованиях. Подсчитайте их количество.

9. В магазине продаются кепки: белые (б), красные (к) и синие (с). Кира и Лена покупают себе по одной кепке. Сколько существует различных вариантов покупок для этих девочек? Перечислите их.

10. Перечислите все двузначные числа, в записи которых встречаются цифры 2, 3 и 4, если:

1) одинаковых цифр в числах нет;

2) цифры в числах могут повторяться.

11. Перечислите все двузначные числа, в записи которых встречаются только цифры 0, 1 и 2, если:

1) одинаковых цифр в числах нет;

2) цифры в числах могут повторяться.

12. Перечислите все трехзначные числа, в записи которых встречаются только цифры 1 и 2.

13. Перечислите все трехзначные числа, в записи которых используются цифры 0, 1 и 2, при условии, что:

1) все цифры в числах различны;

2) цифры в числах могут повторяться.

14. У жителей планеты ХО в алфавите три буквы: А, О, Х. Слова в языке состоят не более чем из трех букв (буква в слове может использоваться любое число раз). Какое наибольшее количество слов может быть в словаре жителей этой планеты?

15. Правила игры ”Детская типография” таковы. Выбираем любое слово - нарицательное имя существительное (желательно с большим числом букв). Все играющие в секрете друг от друга из букв выбранного слова составляют всевозможные новые слова - имена существительные (в новом слове буква используется не чаще, чем она встречается в исходном слове). Побеждает тот, кто за условное время составит больше слов. (В игре ”Взрослая типография” победителем считается тот, у кого больше сумма всех букв в составленных словах.)

Задание. Сыграйте в игру ”Детская типография”, используя слово:

1) полк;

2) комбинаторика.

Таблица вариантов и правило произведения

При решении комбинаторных задач существует опасность потери какой-либо комбинации элементов, поэтому и появились приемы, исключающие эту возможность. Например, дл подсчета числа комбинаций из двух элементов подходящим средством является таблица вариантов.

Пример 11. Записать всевозможные двузначные числа, используя при этом:

1) цифры 1, 2 и 3;

2) цифры 0, 1, 2 и 3. Подсчитать их количество N.

Решение. Для каждого случая составим таблицу вариантов.

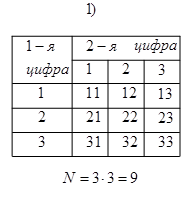
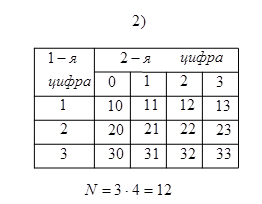
Новое в образовании:

Этапы формирования способностей к изобразительной деятельности
Выявление способностей у детей и правильное их развитие - одна из важнейших педагогических задач. И решаться она должна с учетом возраста детей, психического раз­вития, условий воспитания и других факторов. Развитие способностей у детей к изобразительному искусству только тогда прине­сет свои плоды ...

Научно-методологическое обеспечение деятельности классного руководителя в современной школе
Необходимость поиска новых подходов к научно-методическому обеспечению деятельности классного руководителя обусловлена изменением его статуса и современными требованиями. Актуальной в связи с введением новых образовательных стандартов становится разработка программ воспитания и социализации учащихс ...

Стилизация творческого источника в современном костюме
Коллекции народного костюма, хранящиеся в музеях нашей страны, наглядно демонстрируют фантазию русских людей, их тонкий художественный вкус, изобретательность и мастерство. Безусловно, это стало возможным только благодаря многовековым традициям, бережно хранимым русским народом и передаваемым по на ...