Методические элементы введения комбинаторики

Ответ:

1) N=9;

2) N=12.

Пример 12. Бросают две игральные кости (каждая кость - кубик с отмеченными на его гранях точками от одной до шести, причем на различных разное число точек). Сколько различных пар точек может появиться на верхних гранях костей? https://infratrest.ru jet сваи технология особенности и преимущества технологии jet.

Решение. С помощью составленной ниже таблицы пар выпавших точек можно утверждать, что число всевозможных пар равно .

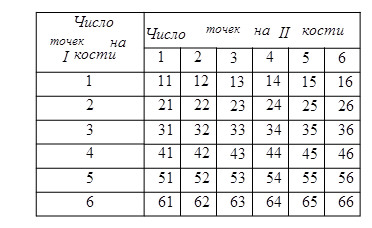
Ответ: 36.

При решении, аналогичных примерам 11 и 12, необязательно каждый раз составлять таблицу вариантов. Можно пользоваться правилом, которое получило в комбинаторике название ”Правило произведения”: если существует n вариантов выбора первого элемента и для каждого из них есть m вариантов выбора второго элемента, то всего существует различных пар с выбранными первым и вторым элементами.

Пример 13. Катя и Оля пришли в магазин, где продаются в любом количестве плитки шоколада трех видов. Каждая девочка хочет купить одну плитку. Сколько существует способов покупки?

Решение. Катя может купить плитку любого из трех видов шоколада (n=3). Аналогично может поступить и Оля (m=3). Пара шоколадок для Кати и для Оли может быть куплена различными способами.

Ответ: 9.

Пример 14. Имеются три различные плитки шоколада. Катя и Оля по очереди выбирают себе по одной плитке. Сколько существует различных способов выбора шоколадок для Катя и Оли?

Решение. Допустим, первой шоколадку выбирает Катя. У нее есть 3 возможности выбора плитки (n=3). После этого Оля может выбрать одну из двух оставшихся плиток (m=2). Тогда способов выбрать пару шоколадок для Кати и для Оли существует .

Ответ: 6.

Пример 15. Сколько существует различных двузначных кодов, составленных с помощью букв А, Б, В, Г и Д, если:

1) буквы в коде могут повторяться;

2) буквы в коде должны быть различны?

Решение.1) Первой буквой в коде может быть любая из данных 5 букв (n=5), второй - также любая из 5 букв (m=5). Согласно правилу произведения число всевозможных пар букв (с возможным их повторением в паре) равно.

2) Первой буквой в коде может быть любая из 5 данных букв (n=5), а второй - любая из 4 оставшихся (m=4). Согласно правилу произведения число двузначных кодов с различными буквами равно .

Ответ:

1) 25;

2) 20.

Упражнения:

1. Используя таблицу вариантов, перечислите все двузначные числа, записанные с помощью цифр:

1) 3, 4, 5;

2) 7, 8, 9.

2. С помощью таблицы вариантов перечислите всевозможные двухбуквенные коды (буквы в коде могут повторяться), в которых используются буквы:

1) а, б, в;

2) x, y, z.

3. Пользуясь таблицей вариантов, перечислите все двузначные числа, в записи которых используются цифры 7, 8, 9.0, и подсчитайте количество этих чисел.

4. Составляя расписание уроков на понедельник для 7 "А" класса, завуч хочет первым уроком поставить либо физику, либо алгебру, а вторым - либо русский язык, либо литературу, либо историю. Сколько существует вариантов расписания на первые два урока?

5. Чтобы попасть из города А в город В, нужно по дороге доехать до реки, а затем переправиться на другой берег. До реки можно доехать на мотоцикле, автобусе, автомобиле или дойти пешком. Через реку можно переправиться либо вплавь, либо на лодке, либо на пароме. Сколько существует различных способов добраться из города А в город В?

6. У Светланы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светланы?

Новое в образовании:

Средства презентации лексики
В методической литературе получил освещение ряд вопросов, связанных с работой над лексикой, в частности способы раскрытия значений ЛЕ. Однако наблюдения за педагогическим процессом обучения ИЯ показал, что проблемы в формировании лексических навыков, необходимых для говорения все же существуют. В в ...

Принцип воспитания и обучения в реальной деятельности, связанной с жизнью
В педагогическом процессе практика или предшествует изучению теоретических положений, или осуществляется после изучения теории для подтверждения истинности полученных знаний и их квалифицированного использования. В некоторых случаях практика является непосредственной целью для воспитанников (учащих ...

Предпосылки развития письменной речи в онтогенезе
Письмо – результат длительной эволюции попыток человека выразить свою мысль не сиюминутно, а продлить ее во времени. В самом начале этого пути человек рисовал то, что хотел сообщить. Затем появились более условные способы: картинка-схема, узелковое письмо, клинопись, иероглифы и, наконец, буквы. Че ...