Методические элементы введения комбинаторики
Рисунок 6
Известно, что составлением магических квадратов увлекались в Древнем Китае несколько тысяч лет назад.
Магического квадрата размером 2 x 2 не существует. Существует единственный магический квадрат размером 3 x 3, внешне отличные от него варианты можно получить либо зеркальным отображением чисел относительно осей симметрии рассмотренного квадрата (их у квадрата 4, см. рис.7), либо поворотом на 900 вокруг центра квадрата (рис.8).
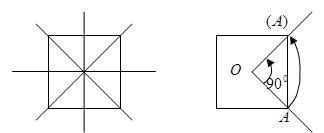
Рисунок 7 Рисунок 8
Пример 5. Составьте магический квадрат, полученный из квадрата, изображенного на рис.6:
зеркальным отображением клеток от горизонтальной оси симметрии квадрата;
поворотом клеток квадрата на 900 вокруг его центра против часовой стрелки.
С увеличением количества клеток, на которые разбит квадрат, увеличивается число возможных магических квадратов.
Например, число всевозможных магических квадратов размером 4 x 4 (с записью в его клетках чисел от 1 до 16 по оговоренным правилам) уже 880, а число магических квадратов размером 5 x 5 более 200 000.
Пример магического квадрата размером 4 x 4 приведен на рис.9.
|
16 |
3 |
2 |
13 |
|
5 |
10 |
11 |
8 |
|
9 |
6 |
7 |
12 |
|
4 |
15 |
14 |
1 |
Рисунок 9
Латинские квадраты
Латинскими называют квадраты размером n x n клеток, в которых записаны натуральные числа от 1 до n, причем таким образом, что в каждой строке и каждом столбце встречаются все эти числа по одному разу. На рис.10 приведен пример латинского квадрата размером 3 x 3.
|
1 |
2 |
3 |
|
2 |
3 |
1 |
|
3 |
1 |
2 |
Рисунок 10
На рис.11, а изображены два латинских квадрата размером 4 x 4, которые имеют такую особенность: если один квадрат наложить на другой (например, второй квадрат считать сделанным из прозрачной бумаги и положить его на первый), то все пары образовавшихся двухзначных чисел (рис.11, б), будут различными. Такие пары латинских квадратов называют ортогональными.
|
1 |
2 |
3 |
4 |
|
2 |
1 |
4 |
3 |
|
3 |
4 |
1 |
2 |
|
4 |
3 |
2 |
1 |
Новое в образовании:
Математические шифры
Занятие по математическим шифрам проводится в виде игры – исторического путешествия (примерное содержание в приложении 14). В начале занятия кратко о шифрах рассказывает учитель, а затем слово предоставляется учащимся. Участники кружка рассказывают о разных шифрах, придуманных в разных странах (Афи ...
Методические основы обучения учащихся прикладным
художественным работам
Определение содержания обучения строилось на основе анализа истории, материальной и духовной культуры русского народа с целью практического использования в учебно-воспитательном процессе. При его отборе и построении решались следующие задачи: определение необходимых для обучения и этнокультурного р ...
Компетентности в структуре личности, педагогической
деятельности и процессе профессионального развития учителя
В отечественной и зарубежной педагогике и психологии накоплен определенный опыт исследований по формированию различных сторон личности будущего педагога, различных направлений его подготовки. Следует отметить, что в основу исследования проблемы формирования личности учителя, его профессиональной по ...