Методические элементы введения комбинаторики

Предлагаемый материал рекомендуется изучать в конце VII класса, исходя из тех соображений, что к этому времени у школьников еще свежи арифметические знания, сохранилась память о предметных действиях, но уже стало очевидным влияние алгебраических и геометрических знаний, т.е. наблюдается стремление к обобщению, алгоритмизации полученной информации, повышается графическая культура. Материал для этого раздела взят из журнала ”Математик в школе".

Основная цель изучения комбинаторики в старшей школе и в вузе - это получение средств решения вероятностных задач. В основной же школе комбинаторика призвана, в основном, сформировать так называемое комбинаторное мышление, позволяющее человеку разумно организовать перебор ограниченного числа данных, подсчитать всевозможные комбинации элементов, составленных по определенному правилу.

В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать количество всевозможных комбинаций элементов, образованных по определенному правилу. Такие задачи называются комбинаторными, а раздел математики, занимающийся решением этих задач, называется комбинаторикой.

Некоторые комбинаторные задачи еще в Древнем Китае, а позднее - в Римской империи. Однако как самостоятельный раздел математики комбинаторика оформилась в Европе лишь в XVIII в. в связи с развитием теории вероятностей.

В древности для облегчения вычислений часто использовали камешки. При этом особое внимание уделялось числу камешков, которые можно было разложить в виде правильной фигуры. Так появились квадратные числа (1, 4, 16, 25, …). На рис.1 показано правило их изображения.

Рисунок 1

Любое n-е по порядку квадратное число вычисляется по формуле

N=n2 (2.2)

Были сконструированы треугольные (1, 3, 6, 10, 15, …) и пятиугольные (1, 5, 12, 22, …) числа.

На рис.2 и 3 показан способ образования этих чисел.

Любое n-e по порядку треугольное число можно найти по формуле

(2.3),

а любое n-e по порядку пятиугольное - по формуле

(2.4).

Рисунок 2

Рисунок 3

Все остальные числа древние математики представляли в виде прямоугольника размером m x n, выложенных из камней, где обязательно m1 и n1 (на рис.6 изображены всевозможные представления составного числа 12). Простые числа представляли в виде линий 1x n (рис.5). В связи с этим составные числа древние ученые называли прямоугольными, а простые - непрямоугольными числами.

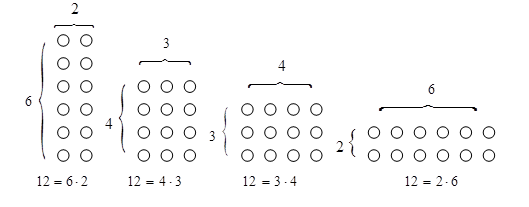
Рисунок 4

Рисунок 5

Пример 4. Найти седьмое по порядку:

1) квадратное число;

2) треугольное число;

3) пятиугольное число.

Решение:

1) по формуле N=n2 при n=7 находим N=72=49.

по формуле при n=7 находим .

по формуле при n=7 находим .

Магические квадраты

Поместим натуральные числа от 1 до 9 в клетках квадрата размером 3 x 3 таким образом, чтобы все суммы чисел по горизонтали и по вертикали, а также по диагоналям были равны 15 (рис.6). Полученный квадрат, а также другие квадраты с теми же свойствами называют магическими квадратами.

Новое в образовании:

Лингвистические особенности лексико-грамматических категорий тюркских языков
Каждый язык имеет свои особенности, свою структурную специфику. Некоторые языки похожи между собой грамматически, другие же резко различаются. Татарский и русский языки принадлежат к разным типам языков, и это накладывает свой отпечаток при изучении татарского. По происхождению языки делят на семьи ...

Приемы работы над сказкой на разных этапах осознавания младших школьников
Восприятие сказки — сложный процесс активного воссоздания образно-предметного и нравственно-смыслового содержания сказки, как особой литературно-художественной формы, способ освоения ребенком социальной действительности. Восприятие сказки, как и игра, составляет один из наиболее значимых видов деят ...

История возникновения программ
Воспитание и обучение в детском саду, осуществляется в соответствии с программой — государственным документом, определяющим цели, задачи и содержание воспитательно-образовательной работы с детьми в дошкольном учреждении. В ней предусмотрена задача всестороннего воспитания дошкольников в соответстви ...