Математический кружок для 5-6 классов как средство развития познавательного интереса


Значимая деталь, изображенная на гравюре «Меланхолия I» – составленный впервые в европейском искусстве магический квадрат 4 Х 4. Сумма чисел в любой строке или столбце равна 34. Два средних числа в нижнем ряду указывают дату создания картины 1514 год.
Размерность квадрата 4*4. Он заполнен числами от 1 до 4*4(16) интересным образом. Учащимся самим предстоит узнать все о магическом квадрате, посчитать, чему равна сумма чисел по любой вертикали, горизонтали и диагонали (34). Учитель, в свою очередь, должен спросить, заметил ли кто-нибудь из них, в каких еще конструкциях встречается данная сумма (сумма встречается в угловых квадратах 2×2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных «ходом коня» (2+8+9+15 и 3+5+12+14), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12).
Магические квадраты
- это таблицы чисел, в которых суммы чисел в каждой строке, в каждом столбце и в каждой из двух диагоналей квадрата все равны между собой.
Из всякого магического квадрата путем различных перестановок составляющих его чисел можно получить множество новых магических квадратов, обладающих теми же свойствами.
Известно, что магических квадратов 2х2 не существует (предложить попытаться составить квадрат 2х2 и доказать, почему же его все таки не существует). Магический квадрат 3х3 только один. Магических квадратов 4х4, как на картине Дюрера, составлено уже 800, а количество магических квадратов 5х5 близко к четверти миллиона!
Заметка в тетрадь: каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n² клеток и называется квадратом n-го порядка.
Рассмотрим удобный способ заполнения магического квадрата 3-го порядка. (Показать, сделанную учителем заранее презентацию, и вместе с ребятами составить магический квадрат третьего порядка по диплому\Магические квадраты.ppt)Наш квадрат разделен на 9 равных клеток. Необходимо расставить в этих клетках числа 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы сумма чисел в каждой строке и в каждом столбике равнялась 15.
1.
Добавим «крылышки» в средний столбец и в среднюю строку.
2.
Выделим по диагоналям клетки, которые мы заполним числами. 3.
Запишем в выделенные клетки числа от 1 до 9. 4.
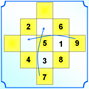
Перенесем числа из «крылышек» во внутреннюю часть квадрата, как показано на рисунках 3, 4, 5.
1.

2.  3.
3. 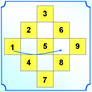 4.
4. 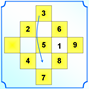 5.
5. 
Участникам кружка предлагается самостоятельно выполнить следующие задания, представленные также в презентации.
Слово учителя.
Магический квадрат Пифагора
«Мир построен на силе чисел», - был уверен великий математик прошлого времени Пифагор, основавший религиозно – философское учение, провозгласившее количественные отношения основой сущности вещей. Он считал, что сущность человека заключается тоже в числе – дате рождения. Поэтому с помощью магического квадрата Пифагора можно познать характер человека, степень отпущенного здоровья и его потенциальные возможности, раскрыть достоинства и недостатки и тем самым выявить, что следует предпринять для его совершенствования.
Пифагор, в своё время, долго жил в племени дагонов, которые, как говорят предания, были не только современниками, но и прилежными учениками древних и таинственных атлантов. Знания, полученные им у дагонов и известные ранее только узкому кругу избранных, учёный сформулировал в своей таблице. По теории дагонов, в дате рождения человека заложена информация о нём и его будущей жизни. Таблица Пифагора позволяет определить, чем природа награждает человека при рождении, в какие обстоятельства он попадёт, как сложится его жизнь. Как известно, Пифагор почитал число превыше всего, он верил, все люди при рождении получают свой номер, который несёт определённую характеристику.
Новое в образовании:
О целесообразности введения теории вероятностей в школе
Существует много аргументов, показывающих важность изучения школьниками элементов теории вероятностей. На данный момент этот вопрос является одним из важнейших аспектов модернизации содержания математического образования, что обусловлено ролью, которую играет вероятностно-статические знания в общео ...
Назначение интерактивных досок
интерактивный доска библиотека Интерактивные доски, произведенные на базе новейших технологий, имеют конкурентоспособную цену. Их использование раскрывает ряд преимуществ при визуализации и коллективном обсуждении документов: - можно выделять элементы из разных документов и программ, вставлять комм ...
Философские, научные основы дидактики
Философской, методологической основой дидактики является диалектический материализм, марксистско-ленинская теория познания, которая раскрывает общие закономерности познания человеком окружающего мира. Диалектический материализм — это наука об общих законах развития природы, общества, мышления челов ...

