Математический кружок для 5-6 классов как средство развития познавательного интереса

Великаны и карлики в мире чисел

1).Сообщение ученика на тему «Легенда о шахматной доске».

2). Рассказ учителя о числах-великанах.

Предложить учащихся вспомнить, какие самые большие числа знают они? (миллион, миллиард, секстиллион …). На данном занятии мы и будем узнавать, какие же самые большие и маленькие числа знает человечество. (таблица с обозначениями числовых великанов и карликов заранее приготовлена и вывешена на доску. Приложение 5).

Самое большое число, название которого удалось отыскать имеет 10100 нулей и называется гуголплекс

!

Для таких "гигантов" придуман сокращенный способ обозначения. Весьма большие числа в научных сочинениях (по астрономии, физике) обозначаются так:

1 000 000=106

10 000 000=107

400 000 000=4·108

6 квадриллионов =6·1015

Теперь давайте разбираться, много ли это, миллион? Тонкость волоса вошла чуть ли не в поговорку. Все часто видят волос и хорошо знают, насколько он тонок.

Толщина человеческого волоса — около 0,07 мм. Мы округлим ее для удобства вычислений до 0,1 мм. Представьте себе, что рядом, бок-о-бок, положен миллион волос. Какой ширины получилась бы полоса. Можно ли было бы например, протянуть ее поперек двери от косяка до косяка?

Если вы никогда не задумывались над такой задачей, то можно поручиться, что, не проделав вычисления, вы дадите грубо-ошибочный ответ. Вы будете, пожалуй, даже оспаривать правильный ответ, — настолько покажется он неправдоподобным. Каков же он?

Оказывается, что ширина полосы из миллиона волос достигала бы примерно ста метров. Ее можно было бы протянуть поперек самой широкой столичной улицы! Это кажется невероятным, но дайте себе труд сделать подсчет, и вы убедитесь, что так и есть: 0,1мм·1 000000 — 0,1м·1000 = 0,1км = 100м (Мы проделали здесь умножение следующим путем: вместо умножения числа, мы дважды заменили самую единицу меры другою, в тысячу раз большею. Этот прием очень удобен для устных подсчетов, и им следует пользоваться).

Задачи для самостоятельного решения:

1).

Сколько времени потребуется человеку, чтобы сосчитать миллиард зерен, если он в минуту будет считать по 100 зерен.

2).

От земли до Марса около 60млн.км. Сколько времени придется лететь на ракете от земли до Марса, если скорость ракеты будет 10км/ч? Сколько времени потребовалось бы самолету, летящему со скоростью 1000км/ч, чтобы преодолеть это расстояние?

3).

В нашей стране проживают около 250 млн. человек. Если все люди встанут в одну шеренгу, то какой длины будет эта шеренга? (Пусть каждый человек занимает место длиной в 50см).

4).

Каких размеров достигает обыкновенный комар, увеличенный в миллион раз? Длина комара приблизительно равна 5мм.

5).

Узнайте свой рост, увеличенный в миллион раз?

6).

Сколько километров займет миллион людей, построенных в один ряд плечом к плечу?

От великанов к карликам.

3). Рассказ учителя о числах - карликах. (Содержания рассказа см. в приложении 5).

В конце занятия обобщим знания, полученные на данном занятии.

Сверхгигант и сверхлилипут.

Наши беседы о великанах и карликах из мира чисел были бы неполны, если не рассказать одной изумительной диковинке этого рода — диковинке, правда, не новой, но стоящей дюжины новинок. Чтобы подойти к ней, начнем со следующей, на вид весьма незамысловатой задачи.

Какое самое большое число можно написать тремя цифрами, не употребляя никаких знаков действий?

Решение:

Хочется ответить: 999,—но, вероятно, вы уже подозреваете, что ответ иной; иначе задача была бы чересчур проста. И, действительно, правильный ответ пишется так:

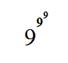
Выражение это означает: "девять в степени девять в девятой степени".

Новое в образовании:

Опытно-экспериментальная работа по формированию культурно-гигиенических навыков у детей младшего дошкольного возраста
Воспитание культурно-гигиенических навыков и навыков самообслуживания являются одним из важнейших направлений воспитательной работы в детском саду. Работа по формированию культурно-гигиенических навыков и навыков самообслуживания должна проводиться как индивидуально, так и группами. Главное условие ...

Особенности внимания младших школьников в психолого-педагогической литературе
Проблема внимания является одной из старейших психологических проблем. Внимание – важное и необходимое условие эффективности всех видов деятельности человека, прежде всего трудовой и учебной. Чем сложнее и ответственнее труд, тем больше требований предъявляет он к вниманию. Внимательность необходим ...

Математический кружок как форма внеклассной работы по математике
Математические олимпиады обычно посвящаются решению задач, но возможны олимпиады по вычислению на счетах, в навыках быстрых и безошибочных подсчетов. Проведение олимпиад должно быть предусмотрено планом работы учителя. Участие детей носит добровольный характер. Олимпиада проводится в 3 тура. В нача ...