Методика изложения теории вероятностей в школе

Можно сказать, что каждый из данных случаев называют событием, и выяснить, какое событие более возможно, менее возможно, есть ли среди данных событий равновозможные. После проведения эксперимента 20 раз и занесения данных в таблицу, следует ожидать более точного совпадения предполагаемого и экспериментально полученного чисел появления каждого из случаев в серии из 40 экспериментов и т.д.

3. Эксперимент, который можно использовать при знакомстве с понятиями: равновозможные события, более вероятное событие, менее вероятное событие.

Оборудование: два белых и один черный шар.

Описание эксперимента. В ящик или мешок кладут два белых и один черный шар. Требуется вытащить последовательно один за другим 2 шара. Учитель спрашивает детей: “Каким может быть результат такого опыта? ”

Обнаруживается, что может быть 3 случая:

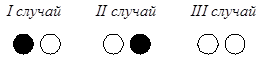
С помощью эксперимента необходимо выяснить, какой из этих случаев более возможен, менее возможен или, может быть, среди них имеются равновозможные случаи. Затем полученные экспериментальные выводы необходимо обосновать, рассмотрев все возможные комбинации выбора двух шаров из имеющихся трех, которые можно условно обозначить Ч, Б1, Б2.

Задачи:

1. Подбрасываются два игральных кубика, подсчитываются суммы выпавших очков (суммы числа очков на верхних гранях обоих кубиков). Сумма выпавших очков на двух кубиках может меняться от 2 до 12. Записать полную группу событий в этом опыте.

2. Сколько элементарных исходов благоприятствует событию “на обоих кубиках выпало одинаковое число очков" при подбрасывании двух игральных кубиков.

3. Подбрасывается два игральных кубика. Какому событию благоприятствует больше элементарных исходов: “сумма выпавших очков равна 7”, “сумма выпавших очков равна 8”?

4. Подбрасывается три игральных кубика, подсчитываются суммы очков, выпавших на них. Сколькими способами можно получить в сумме 5 очков; 6 очков?

5. Три сестры - Ольга, Маша и Таня - тянут жребий, кому из них мыть посуду. Для этого они кладут в шапку три бумажки, на которых нарисован крестик, и по очереди их вытаскивают: Ольга - первая, Маша - вторая, Таня - третья. Выпишите все возможные исходы этого опыта и найдите их количество.

4. Историческая справка: для разнообразия в обучении можно рассказать о теории вероятностей.

Вероятность - характеристика степени появления некоторого события при тех или иных определенных условиях.

Классическая теория вероятностей рассматривает вероятность как отношение числа благоприятствующих случаев ко всем возможным. При этом предполагается, что все рассмотренные случаи являются равновозможными, равновероятными. Так, если мы берем идеально изготовленную шестигранную игральную кость, то у нас нет оснований считать, что она на какую-то из граней будет выпадать чаще, чем на другую; более того, есть все основания для того, чтобы считать равновероятным выпадение ее на каждую из граней. Поэтому при бросании такой кости выпадение каждой из них можно ожидать с вероятностью, равной 1/6. В классической теории вероятностей мы имеем дело со случаями, когда вычисленная чисто теоретически вероятность того или иного события подтверждается в процессе опытной проверки. Такая ситуация, основывающаяся на симметричности исходов опыта, сравнительно редко встречается при исследовании реальных событий в науке и практике. Теория частотной, или статистической, вероятности, у истоков которой стояли Р. Мизес и Г. Рейхенбах, преодолевает указанную ограниченность классической теории.

Ключевым в частотной теории является понятие относительной частоты. Это отношение числа появлений изучаемого события в серии испытаний в данных условиях к числу всех испытаний, в которых это событие могло бы появиться при тех же условиях. Частотная теория позволяет по результатам относительной частоты изучаемых массовых случайных событий судить об их вероятности. Применение математики к изучению событий такого характера опирается на то, что во многих случаях при многократном повторении испытаний в примерно равных условиях частота появления результата остается примерно одинаковой. Результат же представляет собой отношение числа опытов, в которых он имел место, к общему числу производимых опытов. Так частота попадания в цель для данного стрелка в одних и тех же условиях при значительном числе испытаний остается почти одной и той же. Процент бракованных изделий в данном ряду испытаний в одном и том же производстве при одинаковых условиях примерно один и тот же.

В последнее время разрабатывается логическая (индуктивная) теория вероятности, в которой изучается отношение между посылками и заключением в правдоподобных умозаключениях. Логическая вероятность характеризует разумную степень веры в появление некоторого события в условиях некоторой неопределенности. Логическая вероятность используется в вероятностной и индуктивной логике.

Новое в образовании:

Диагностика физического развития детей дошкольного возраста
Физическое развитие – это комплекс функциональных и морфологических свойств организма, который определяет запас его физических сил. Для детей и подростков его следует расширить с учетом тех биологических процессов, которые наиболее характерны для детского организма, а именно – его роста и формирова ...

Особенности школьного туризма
В школьном туризме (в противоположность семейному) действуют две стороны – участвующая (школьники) и организующая, содействующая (администрация, учителя школы). По этому признаку школьный туризм занимает промежуточное положение между плановым и самодеятельным туризмом. У школьников и у учителей отн ...

Исследование влияния межпредметных связей на эффективность процесса обучения
Экпериментальная работа проводилась в общеобразовательной средней школе № XX г. XXXXXXX. В 5 классе «А» 22 учащихся: 11 мальчиков и 11 девочек. Класс учится по типовой программе. Учитель ОБЖ имеет высшее педагогическое образование, высшую квалификационную категорию. Констатирующий эксперимент. Цель ...