Элементы комбинаторики. Принцип Дирихле

В начале занятия кратко рассказать историю зарождения комбинаторики и об областях ее применения.

Определение. Задачи на составление числа возможных соединений элементов с определенными свойствами, которые можно составить из элементов заданного множества, называются комбинаторными.

Задача 1.

Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?

Решение: Для того чтобы не пропустить и не повторить ни одно из чисел, будем выписывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7. Получаем следующий расклад.

Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел. Данный метод называется методом перебора

.

Однако существует другой подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название –

дерево возможных вариантов

.

Вернемся к задаче о составлении двузначных чисел из цифр 1, 4 и 7. Для ее решения можно построить специальную схему.

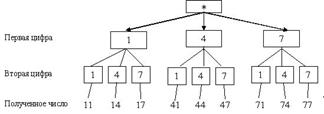
Эта схема действительно похожа на дерево, правда, "вверх ногами" и без ствола. Знак “*” изображает корень дерева, ветви дерева – различные варианты решения. Чтобы получить двузначное число, надо сначала выбрать первую его цифру, а для нее есть три варианта: 1, 4 или 7. Поэтому из точки * проведены три отрезка и на концах поставлены цифры 1, 4 и 7.

Теперь надо выбрать вторую цифру, а для этого также есть три варианта: 1, 4 или 7. Поэтому от каждой первой цифры проведено по три отрезка, на концах которых снова записано 1, 4 или 7. Итак, получено всего 9 различных двузначных чисел. Других двузначных чисел из этих трех цифр составить невозможно.

Дополнительная подзадача:

Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры десятков и единиц не повторяются?

Задача 2.

Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

Способ 1: Обозначим города их первыми буквами. Тогда код каждого маршрута будет состоять из трех букв: В, Р и Ф, каждая из которых должна быть использована только один раз, например, ВФР или ФРВ.

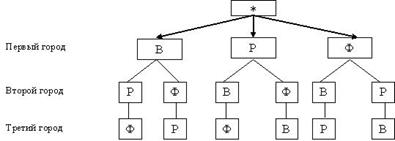
Варианты путешествия получаются следующие: ВРФ, ВФР, РВФ, РФВ, ФВР, ФРВ

, что хорошо видно из дерева вариантов.

Путешествие можно начинать в любом из трех городов. Если первой посетить Венецию, то затем можно поехать в Рим или во Флоренцию. Если вторым посетить Рим, то третьей будет Флоренция, если второй будет Флоренция, то третьим будет Рим. Это первые два варианта путешествия. Таким образом, всего существует 6 вариантов путешествия.

Новое в образовании:

Формирование адаптивных качеств учащихся
Одна из функций работы социального педагога в общеобразовательной школе — помощь детям в сложном процессе их социализации, выработ­ка у них социоадаптивных качеств, помогаю­щих справиться с трудными ситуациями любо­го уровня и позволяющих не только приспособиться к жизни, но и реализовать свой твор ...

Время как фактор успешности учения
Какое влияние оказывает время на успешность учебы школьников? Для педагогов такая постановка нова. Мы все больше имели дело со временем социальным, внешним по отношению ко внутреннему, определяющему познавательный процесс ребенка, и потому соотносили его с деятельностью педагогов и учением. В этом ...

Исследование досуговых предпочтений детей г. Волгограда
Цель нашего исследования – выявить досуговые предпочтения учащихся школ г. Волгограда и проанализировать результаты проведённого нами социологического обследования. Анкетным опросом было охвачено 700 детей и 300 родителей г. Волгограда. В бюджете времени учащихся обычно выделяют учебное и внеучебно ...