Графы. Применение графов к решению задач

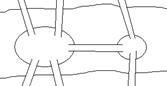
Попробуем разрешить эту задачу. Но сначала составим план города, как это сделал Л.Эйлер. Он обозначил части города точками (вершины), а переходы по мостам – линиями (ребра). Получил граф.

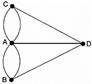
Ответ: обход по всем мостам только один раз невозможен, т.к. все вершины графа нечетные.

Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.

Задачи для самостоятельного решения:

1). Алина решила маме на день рождения подарить букет цветов (розы, тюльпаны или гвоздики) и поставить их или в вазу или в кувшин. Сколькими способами это можно сделать?

2). Ранним утром Миша Маша, Андрей обменялись приветствиями каждый с каждым. Сколько всего было приветствий. Решите задачу с помощью графа. Нарисуй граф в рабочей тетради.

3).

В квартирах №1,2,3 жили три друга: Айдар, Тима и Саша. Известно, что в квартирах №1 и 2 жил не Айдар. Тима жил не в квартире №1. В какой квартире жил каждый из друзей.

4).

Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?

5).

Какие буквы русского алфавита можно нарисовать одним росчерком?

6).

Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все 12 ребер куба, не проходя дважды по одному ребру. Подпрыгивать и перелетать с места на место не разрешается.

Новое в образовании:

Сущность концепции совершенствования технологической подготовки будущих учителей
Концепция высшего педагогического технологического образования, включающая переосмысление как содержательного компонента, так и его структурных частей, предполагает обновление методологических, психолого-педагогических и методических подходов к технологической подготовке, направленных на повышение ...

Результаты исследования и их анализ
Методика 1 – Составление рассказа по картинке . Цель: определить уровень развития связной монологической речи. Инструкция. Я покажу тебе картинку. Придумай рассказ: что происходит, о чем говорят, что будет потом. Если ребенок затрудняется в описании, можно ему помогать, задавая наводящие вопросы. Н ...

Понятие о декоративности
Слова «декоративность», «декорация» происходят от латинского слова «decoro», что значит «украшать». Сама природа как будто наделяет свои создания не только полезными свойствами, но и красотой. «Феникс щеголяет красотой оперения, индюк надувает и делает ярким зоб, тигр и леопард привлекают внимание ...