Графы. Применение графов к решению задач
Графы
– это рисунки, которые состоят из точек и линий, соединяющих эти точки.
Каждая пара точек в графе может быть соединена линиями
. Линия указывает на связь между двумя точками
. Точки называются вершинами графа
, а линии - рёбрами.
С какими графами вы встречаетесь повседневной в жизни? (схемы авиалиний, которые часто вывешивается в аэропортах, схемы метро, а на географических картах – изображение железных дорог). С помощью графов изображаются схемы дорог, газопроводов, тепло и электросетей.
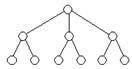
Особым видом графа является дерево. Дерево (граф
) – это способ организации информации об отношениях между объектами, в нем нет циклов, то есть нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину. Примером такого дерева может служить генеалогическое дерево Рюриковичей и Романовых.

Рассмотрим одну из простейших задач: Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Венера; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты изобразим точками, их у нас 9, а маршруты ракет – направляющими линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.
Запишем еще одно определение: Степенью вершины графа
называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
1). В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?
Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным15·5/2=37,5. Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
Ответ. Соединить телефоны таким образом невозможно.
2).
В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение. Подсчитаем общее количество выходящих городов дорог – 100 . 4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.
4).
Обрисовать фигуру, не отрывая карандаша от бумаги и не проводя два раза по одной линии. Обозначьте точки пересечения, в скобках укажите, сколько линий выходит из данной точки. Если число линий четное – то вершина четная, если число линий нечетное – то вершина нечетная. Пометить вершину, с которой надо начинать обход.
1.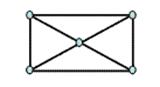 2.
2.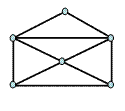 3.
3.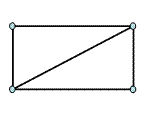 4.
4.
Все ли фигуры у вас получилось нарисовать? (все, кроме фигуры №1). Как вы думаете почему? Как это связано с количеством четных и нечетных вершин?
Сделаем вывод:
· Если все вершины графа четные, то нарисовать фигуру возможно, и начать можно с любой вершины (№4).
· Если же из этих вершин две нечетные, то нарисовать фигуру можно, но только начинать необходимо в одной из этих двух нечетных вершин, а заканчивать во второй нечетной вершине (№2, №3).
· Если в графе более двух нечетных вершин, то нарисовать фигуру невозможно (№1).
Вопрос о разрешимости таких задач входит в теорию графов. Впервые ее исследовал Л.Эйлер в 1736г., решая задачу о Кенигсбергских мостах.
5).
Город Кенигсберг расположен на берегах и двух островах реки Преголя. Части города соединены между собой семью мостами. В воскресные дни горожане совершили прогулки по городу. И возник вопрос, можно ли выбрать такой маршрут, чтобы пройти по каждому мосту только один раз и вернуться в начальную точку пути?
Новое в образовании:
Содержание работы по оригами на уроках труда
Курс занятий по обучению оригами целесообразней осваивать в 3 этапа (примерно 4 года обучения). В процессе обучения постепенно возрастает уровень сложности выполняемых детьми работ. Многие фигурки, известные в оригами, начинают складывать одинаково до определенного момента. Одинаковые заготовки наз ...
Моделирование дидактической системы формирования логической культуры
мышления у младших школьников
В нашей стране моделирование как метод педагогического исследования стал разрабатываться с конца 60-70-х годов XX века. Практика развивающегося народного образования требовала, чтобы с самого начала педагог обладал точным научным представлением о процессе и результатах обучения и воспитания. В связ ...
Организация обмена данными. Редактирование текста
Цель: Формировать навыки простейшего редактирования текста: вставка и удаление слов, удаление лишних символов, напечатание недостающих символов, вставка и удаление пустых строк, копирование и вставка слов. Ход урока Организационный момент. Повторение пройденного. Каково основное назначение текстово ...

