Круги Эйлера

1. Примерное содержание сообщения учащегося о Леонарде Эйлере.

2. Рассказ учителя о кругах Эйлера.

Очень часто бывает так, что решение задачи помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным.

Рассмотрим такую задачу.

1).

В классе 35 учеников. Из них: 19 ребят занимают в математическом кружке, 10 – в биологическом, 9 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?

Решение. Для решения задачи изобразим в виде «кругов» учащихся, занимающихся математикой и биологией.

Обозначим их буквами М и Б соответственно. Круги М и Б содержатся в прямоугольнике, которым мы изображаем всех учащихся класса.

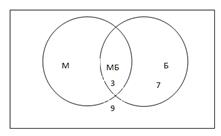
Нам очевидно, что общая часть кругов М и Б состоит из тех ребят, которые одновременно увлекаются и математикой, и биологией. Теперь давайте посчитаем. Всего внутри прямоугольника 35 ребят. Внутри двух маленьких кругов М и Б будет 35-9= 26 ребят, поскольку нам известно, что 9 ребят не посещают кружки. Внутри «математического» круга 19 ребят, значит, в той части «биологического» круга, которая расположена вне круга М, находится 26-19= 7 биологов, не посещающих математический кружок. Остальные биологи, их 10-7= 3, находятся в общей части кругов МБ. Таким образом, 3 биолога увлекаются математикой.

Изображение различных множеств в виде кругов широко использовал в своих научных трудах великий математик ХVIII века Леонард Эйлер. Именно поэтому рисунки, подобные в задаче, которую разобрали выше, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения».

Круги Эйлера

— геометрическая схема, с помощью которой можно изобразить отношения между подмножествами.

2).

В киоске около школы продается мороженое двух видов: «Спортивное» и «Мальвина». На перемене 24 ученика успели купить мороженое. При этом 15 из них купили «Спортивное», а 17 – мороженое «Мальвина». Сколько человек купили мороженое обоих сортов?

Решение. Попробуем изобразить данные задачи с помощью кругов.

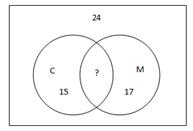
Общая часть кругов состоит из тех школьников, которые купили мороженое обоих сортов. Всего мороженое купили 24 ученика. Внутри круга М 17 учеников, а в круге С – 15 учеников. Возьмем, например, учащихся, купивших мороженое «Мальвина». Получим 24-17=7 учащихся, которые купили мороженое «Спортивное», но не купили мороженое «Мальвина». Остальные учащиеся: 15-7= 5 купили и мороженое «Спортивное», и «Мальвина». Таким образом, мы получили 5 учеников, которые купили оба вида мороженого.

3).

Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?

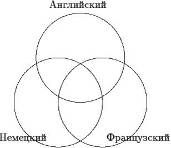
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языками владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.

Новое в образовании:

Работа с географическими терминами для совершенствования коррекционной работы по речевым недостаткам детей - олигофренов
Развитие речи умственно отсталых учащихся -одна из важнейших задач, которая решается вспомогательной школой в процессе преподавания всех учебных предметов. Столь пристальное внимание к речевому развитию детей не случайно. Работая над исправлением различных нарушений речи, формируя речевые умения и ...

Дидактическая игра - как средство воспитания звуковой культуры речи детей дошкольного возраста
Дидактическая игра (игра обучающая) – это вид деятельности, занимаясь которой дети учатся. Она, как и каждая игра, представляет собой самостоятельный вид деятельности, которой занимаются дети: она может быть индивидуальной или коллективной. Данная игра является ценным средством воспитания действенн ...

Понятие о декоративности
Слова «декоративность», «декорация» происходят от латинского слова «decoro», что значит «украшать». Сама природа как будто наделяет свои создания не только полезными свойствами, но и красотой. «Феникс щеголяет красотой оперения, индюк надувает и делает ярким зоб, тигр и леопард привлекают внимание ...