Задачи на разрезание и перекраивание фигур

Вступительное слово учителя:

Небольшая историческая справка: Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих простых задач на разрезание были найдены еще древними греками, китайцами, но первый систематический трактат на эту тему принадлежит перу Абуль-Вефа. Геометры всерьез занялись решением задач на разрезание фигур на наименьшее число частей и последующее построение другой фигуры в начале 20 века. Одним из основателей этого раздела был знаменитый основатель головоломок Генри Э.Дьюдени.

В наши дни любители головоломок увлекаются решением задач на разрезание прежде потому, что универсального метода решения таких задач не существует, и каждый, кто берется их решать, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению. (На занятии мы будем указывать лишь один из возможных примеров разрезания. Можно допустить, что у учащихся может получиться какая-то другая верная комбинация — не надо этого бояться).

Данное занятие предполагается провести в виде практического занятия. Разбить участников кружка на группы по 2-3 человека. Каждой из групп предоставить заранее подготовленные учителем фигуры. Учащиеся располагают линейкой (с делениями), карандашом, ножницами. Разрешается производить с помощью ножниц лишь прямолинейные разрезы. Разрезав какую-нибудь фигуру на части, необходимо составить другую фигуру из тех же частей.

Задачи на разрезание:

1).

Попробуйте разрезать изображенную на рисунке фигуру на 3 равные по форме части:

Подсказка: Маленькие фигуры очень похожи на букву Т.

Ответ: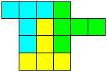

2). Разрежьте теперь эту фигуру на 4 равные по форме части:

Подсказка: Легко догадаться, что маленькие фигурки будут состоять из 3 клеточек, а фигур из трех клеточек не так много. Их всего два вида: уголок и прямоугольник.

Ответ:

3).

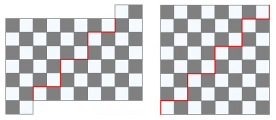
Разделите фигуру на две одинаковые части, и из полученных частей сложите шахматную доску.

Подсказка: Предложить начать выполнять задание со второй части, как бы получить шахматную доску. Вспомнить, какую форму имеет шахматная доска (квадрат). Посчитать имеющееся количество клеточек в длину, в ширину. (Напомнить, что клеток должно быть 8).

Ответ:

4). Попробуйте тремя движениями ножа разрезать сыр на восемь равных кусков.

Подсказка: попробовать разрезать сыр вдоль.

Ответ: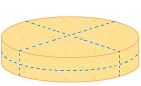

Задачи для самостоятельного решения:

1).

Вырежьте квадрат из бумаги и выполните следующее:

· разрежьте на такие 4 части, из которых можно составить два равных меньших квадрата.

· разрежьте на пять частей – четыре равнобедренных треугольника и один квадрат – и сложите их так, чтобы получилось три квадрата.

3).

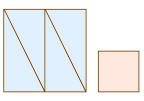
Перед вами два квадрата, один из которых уже разделен на четыре одинаковых треугольника. Как при помощи этих треугольников и маленького квадрата сложить один большой квадрат? Ничего больше разрезать не требуется.

4).

На рисунке изображена фигура в виде запятой. При помощи одной кривой линии разделите эту фигуру на две одинаковые части. Какую геометрическую фигуру можно сложить из двух таких фигур ("запятых")?

5).

У одной из сестер милосердия, было пять кусков красной материи, из которых она, используя все эти куски и не разрезая их более, сшила крест. Как она это сделала?

В конце занятия предложить учащимся просмотреть презентацию с заданиями. (презентация).

Новое в образовании:

Анализ программы подвижных игр в комплексной программе физического воспитания начальной школы
Подвижные игры в начальной школе являются незаменимым средством решения комплекса взаимосвязанных задач воспитания личности младшего школьника, развития его разнообразных двигательных способностей и умений. Многообразие двигательных действий, входящих в состав подвижных игр, оказывает комплексное в ...

Анализ содержания сказки
Алгоритм анализа содержания сказки можно представить следующим образом: 1. Тема сказки (например, про любовь, про животных, и др.). Отмечается оригинальность или заимствованность сюжета, влияние внешней среды на творчество. 2. Анализ героев и образов. Выделяются главные и вспомогательные. Герои кла ...

Научно-методологическое обеспечение деятельности классного руководителя в современной школе
Необходимость поиска новых подходов к научно-методическому обеспечению деятельности классного руководителя обусловлена изменением его статуса и современными требованиями. Актуальной в связи с введением новых образовательных стандартов становится разработка программ воспитания и социализации учащихс ...